Árboles Auto Balanceados

AVL

Un árbol AVL o de Adelson-Velsky y Landis, es un árbol binario de búsqueda autobalanceado

Si el factor de balanceo de algún nodo del árbol es en módulo mayor a 1, entonces es necesario reequilibrar

Rotaciones

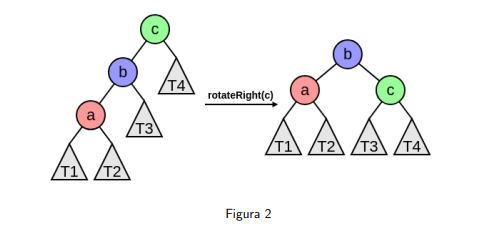
• Rotación Simple a Derecha: Ocurre cuando el factor de balanceo del nodo $FE=-2$ y el factor de balanceo del hijo izquierdo $FE=0,-1$.

  Entonces rotamos hacia la derecha el nodo desbalanceado

  

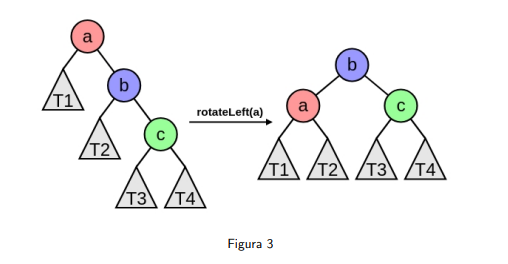
• Rotación Simple a Izquierda: Ocurre cuando el factor de balanceo del nodo $FE=2$ y el factor de balanceo del hijo izquierdo $FE=0,1$.

  Entonces rotamos hacia la izquierda el nodo desbalanceado

  

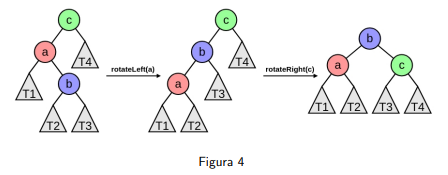
• Rotación Izquierda - Derecha: Ocurre cuando el factor de balanceo del nodo $FE=-2$ y el factor de balanceo del hijo izquierdo $FE=1$.

  Entonces rotamos hacia la izquierda el nodo hijo, y hacia la derecha el nodo desbalanceado.

  

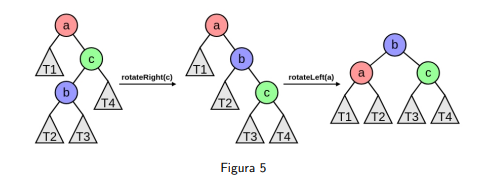
• Rotación Derecha - Izquierda: Ocurre cuando el factor de balanceo del nodo $FE=2$ y el factor de balanceo del hijo izquierdo $FE=-1$.

  Entonces rotamos hacia la derecha el nodo hijo, y hacia la izquierda el nodo desbalanceado.

  

Inserción

Utilizamos el algoritmo usual de inserción de elemento en un árbol binario, Pero una vez insertado calculamos las alturas de los padres y aplicamos los balanceos necesarios. Los balanceos le reducen la altura a una rama en uno, por lo que después de aplicar alguna de las rotaciones vistas anteriormente no es necesario seguir rotando.

Si insertamos un elemento modificamos el factor de balanceo de su padre en uno, Luego le sumamos este factor de balanceo a su padre y así sucesivamente hasta encontrar un desbalance.

Es decir, si algún nodo llega a $FE=0$, entonces no es necesario seguir calculando factores de balanceo.

Eliminación

Utilizamos el algoritmo usual de eliminación de elemento en un árbol binario, Pero una vez eliminado, calculamos las alturas de los padres y aplicamos los balanceos necesarios.

A cada nodo le modificamos el factor de balanceo en uno hasta que encontramos un desequilibrio, o hasta que verificamos que la eliminación del nodo ha dejado de repercutir en la altura del subárbol.

En el borrado a veces es necesario aplicar más de una rotación.

Árbol Rojo y Negro

Un árbol Rojo-Negro es un árbol binario de búsqueda autobalanceado. Cada nodo de este árbol posee una información extra que es el color del nodo.

Para que este tipo de árbol sea válido se tienen que cumplir los siguientes requisitos:

• Todo nodo es o bien rojo o bien negro
• La raíz es negra
• Todas las hojas son negras
• Todo nodo rojo debe tener dos nodos hijos negros
• Cualquier camino desde un nodo dado a sus hojas contiene el mismo número de nodos negros

El número de nodos negros desde el nodo raíz a un nodo es denominado la profundidad negra del nodo. El número uniforme de nodos negros en todos los caminos, desde la raíz hasta las hojas, se denomina altura-negra. De esta forma, se cumple que

El camino más largo desde la raíz hasta una hoja no es más largo que dos veces el camino más corto desde la raíz a una hoja. Como resultado, el árbol está aproximadamente equilibrado

Machete Arbol RN.pdf

Árbol B

Los árboles B de búsqueda nacen a partir de la necesidad de tener un número muy grande de elementos, en estos árboles se prioriza la poca profundidad.

Para que un árbol B de orden $k$ sea válido se tienen que cumplir los siguientes requisitos:

• La cantidad mínima de claves es al menos $k/2$ (excepto raíz)
• Un nodo con $k$ claves tiene, como máximo, $m=k+1$ descendientes
• La cantidad mínima de descendientes es $m/2$ (excepto raíz y hojas)

Búsqueda

La búsqueda se hace partiendo el nodo inicial, evaluando en que rama del nodo debería estar, y repitiendo hasta llegar a un nodo nulo o al elemento buscado.

Inserción

Los elementos en un árbol B se insertan siempre en las hojas. El algoritmo de inserción en un árbol B sigue los siguientes pasos:

1. Buscar el nodo donde debería ser insertada la nueva clave
2. Si el nodo no está completo, entonces insertar el valor respetando el orden
3. Si el nodo está lleno, entonces lo insertamos en el conjunto existente de clave, dividimos el nodo en dos y movemos el elemento del medio hacia el nodo padre. Si el nodo padre está lleno, repetir.

Eliminación

Al igual que la inserción, la eliminación se realiza desde los nodos hojas.

Caso 1: Eliminación de un nodo hoja.

1. Buscamos el nodo donde se encuentra el elemento a eliminar
2. Si el nodo contiene más claves que el número mínimo de claves, simplemente lo elimina
3. Si el nodo contiene el número mínimo de claves, lo quita y toma un elemento del hermano
   1. Si el hermano de la derecha tiene más elementos que el mínimo número de claves, remplaza el elemento siguiente del nodo padre con la menor clave del hermano izquierdo y baja el elemento remplazado al nodo actual.
   2. Si el hermano de la derecha tiene el mínimo número de claves, tomamos del hermano izquierdo
4. Si no se puede tomar elementos de los hermanos, entonces se crea un nuevo nodo combinando dos nodos hermanos y el elemento en el medio. Si el nodo padre se queda con menos elementos que el mínimo, entonces repetimos el proceso en el nodo padre.

Caso 2: Eliminación de un nodo interno.

En este caso, intercambiamos el elemento a eliminar con su sucesor o predecesor hasta que la clave a eliminar se encuentre en las hojas. Luego seguimos los pasos del caso anterior.

Heap

El heap es un árbol binario, puede ser tanto maximal como minimal. Los nodos hijos son siempre menores que los padres, pero no hay relación entre hermanos. Si es maximal, el mayor elemento se encuentra en la raíz. Si es minimal, el menor elemento se encuentra en la raíz.

Otra propiedad del heap es que es un árbol casi completo. Esto quiere decir que el último nivel es el único que puede tener elementos faltantes. Además, los elementos faltantes están todos agrupados del lado derecho del nivel.

Inserción

Para insertar, insertamos el elemento en el primer lugar disponible, luego lo intercambiamos con el nodo padre si es necesario. Repetimos esta operación hasta que el heap esté ordenado. Esta operación se llama sift up. Este algoritmo tiene complejidad $\log n$

Eliminación

En el heap binario, solo podemos borrar la raíz. Para hacerlo, lo quitamos y lo remplazamos con el último elemento, luego lo intercambiamos con el hijo adecuado (el mayor en un heap maximal). Repetimos esta operación hasta que el heap esté ordenado. Esta operación se llama sift down. Este algoritmo tiene complejidad $\log n$

Construcción

Este algoritmo parte de un conjunto de valores y construye un heap. Para esto, numeramos cada uno de los nodos de izquierda a derecha, arriba a abajo. Relacionamos los nodos hijos y padres de forma matemática, de esta forma representamos el heap como un vector.

$$N:\text{Nodo Actual}⟹\{\begin{array}{l}2N+1:\text{Hijo Izquierdo}\\ 2N+2:\text{Hijo Derecho}\end{array}$$

Entonces, si tenemos una lista de elementos y queremos convertirla en un heap, lo que hacemos es tomar el vector y suponemos que tenemos un heap con un solo elemento (ignoramos el resto de elementos del vector). Luego vamos aumentando el tamaño del heap y aplicándole sift up a cada nuevo elemento. Esta operación se llama heapify.

Este algoritmo tiene complejidad $n\log n$

Este algoritmo crea un heap a partir del conjunto de valores inicial, sin usar memoria auxiliar. Este tipo de algoritmos se denomina in-place.

Otra forma de hacer un heapify, es partir del último elemento del vector y aplicar sift down a todos los elementos hasta llegar al inicio.

Heap Sort

Es un algoritmo de ordenamiento que se aprovecha de la construcción de un heap. Para esto, primero aplicamos heapify en el vector. Luego, retiramos la raíz sucesivamente hasta que nos quedemos sin elementos. Así obtenemos un algoritmo de ordenamiento $n\log n$.

Podemos almacenar los números eliminados del heap al final del arreglo, de esta forma no usamos memoria adicional.