Un algoritmo recursivo es aquel que se llama a sí mismo, hay distintos tipos de recursividad:
- Recursividad Directa
- Recursividad Indirecta
- Recursividad de Cola
La recursividad se puede aplicar para resolver problemas que son resolubles mediante una solución de una nueva instancia del mismo problema
Recursividad Directa
El algoritmo de recursividad directa es aquel que se llama a sí mismo, directamente. Una función recursiva debe cumplir con ciertas reglas para que funcione correctamente:
- Debe poseer una condición de corte
- Debe poseer una llamada recursiva
Ámbito
El ámbito de una función es la región de memoria del stack a la que él puede acceder. Dentro del ámbito de una función se almacenan:
- Los argumentos que son pasados a la función
- Las variables declaradas en la función
- La línea a la que debe regresar una vez completada la ejecución.
Recursividad Indirecta
El algoritmo de recursividad indirecta es aquel que no se llama a sí mismo, sino que llama a otra función, la cual llama a la función original.
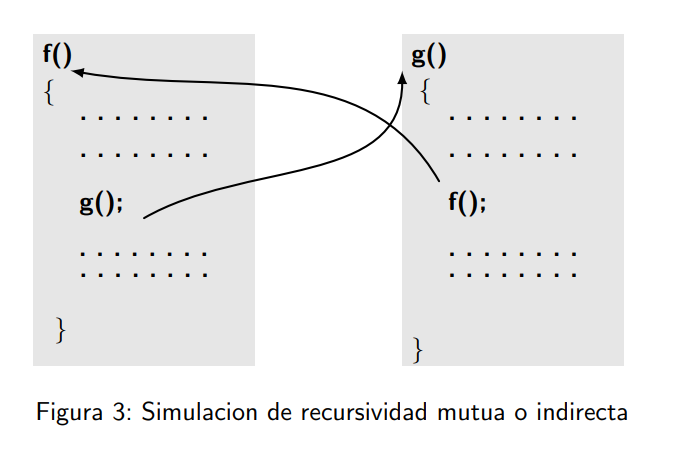
Para lograr esto, en C se debe declarar la firma de las funciones de antemano, para que el compilador las detecte.
Recursividad de Cola
La recursividad de cola es aquella que la última función que ejecuta es la llamada recursiva. De esta forma, se puede descartar la memoria almacenada al final de cada llamada, para optimizar más el uso del stack.
// Un ejemplo de un alguritmo factorial, recursivo de cola.
int factorial_rec (int n, int parcial)
{
if(n == 0)
{
return parcial ;
}
return factorial_rec (n - 1 , parcial * n );
}
int factorial (int n)
{
return factorial_rec (n, 1) ;
}Divide y Conquista
El método divide y conquista es una forma general no solo de solucionar problemas, sino también de diseñar algoritmos.
Está compuesto por tres fases:
- Dividir: el problema es un número de subproblemas, que sean instancias menores del mismo problema
- Conquistar: los subproblemas de modo tal que sean resueltos recursivamente, hasta que el tamaño del problema sea lo suficientemente pequeño como para que su solución sea simple (caso base)
- Combinar: las soluciones obtenidas por cada subproblema en la solución del problema original