Operaciones entre Grafos

Existen 257 operaciones entre grafos, pero trabajaremos únicamente con cuatro de ellas.

Potencia

Sea $G$ un grafo finito simple, entonces definimos denotamos el grafo potencia como $G^q$, donde

$$V(G^q)=V(G)$$ $$u,v\in E(G^q)⟺d_G(u,v)\le q$$

Observemos algunos ejemplos:

$$K_4=P_4^3$$ $$C_5^2=K_3$$ $$C_6^2=3\text{-Cocktail}$$

El grafo conocido $p$-Cocktail cumple que todos los vértices se conectan con todos los grafos, excepto uno (su pareja). $p$ representa el número de parejas.

Suma (Disjunta)

Definimos la operación de suma disjunta entre $G$ y $H$ como $G+H$, donde

$$V(G+H)=V(G)+V(H)$$ $$E(G+H)=E(G)+E(H)$$

La suma repetida se denota como $kG=\underset{\text{k veces}}{\underbrace{G+G+\cdots +G}}$

Observemos algunos ejemplos:

$$C_6^2=(3P_2{)}^{\prime }$$ $$(4N_4{)}^{\prime }=K_4$$

Ensamble

Definimos la operación de ensamble (o join) entre $G$ y $H$ como $G\ast H$, donde

$$V(G\ast H)=V(G)+V(H)$$ $$E(G\ast H)=E(G)+E(H)+\{\{u,v\}:u\in G,v\in H\}$$

Observemos algunos ejemplos:

$$P_2\ast P_2=K_4$$ $$N_1\ast N_{n-1}=S_n$$ $$N_1\ast C_{n-1}=W_n$$

Producto Cartesiano

Definimos la operación de producto cartesiano entre $G$ y $H$ como $G\times H$, donde

$$V(G\times H)=V(G)\times V(H)$$

Luego, $\forall u,w\in V(G)$, $\forall v,h\in V(H)$, entonces

$$\begin{array}{c}(u,v)(w,h)\in E(G\times H)⟺\\ (u=w\wedge (v,h)\in E(H))\vee (v=h\wedge (u,w)\in E(G))\end{array}$$

Observemos que $n(G\times H)=n(G)\cdot n(H)$, y que $m=n(H)m(G)+n(G)m(H)$

Un ejemplo podría ser el de la telaraña $W_{n,m}$:

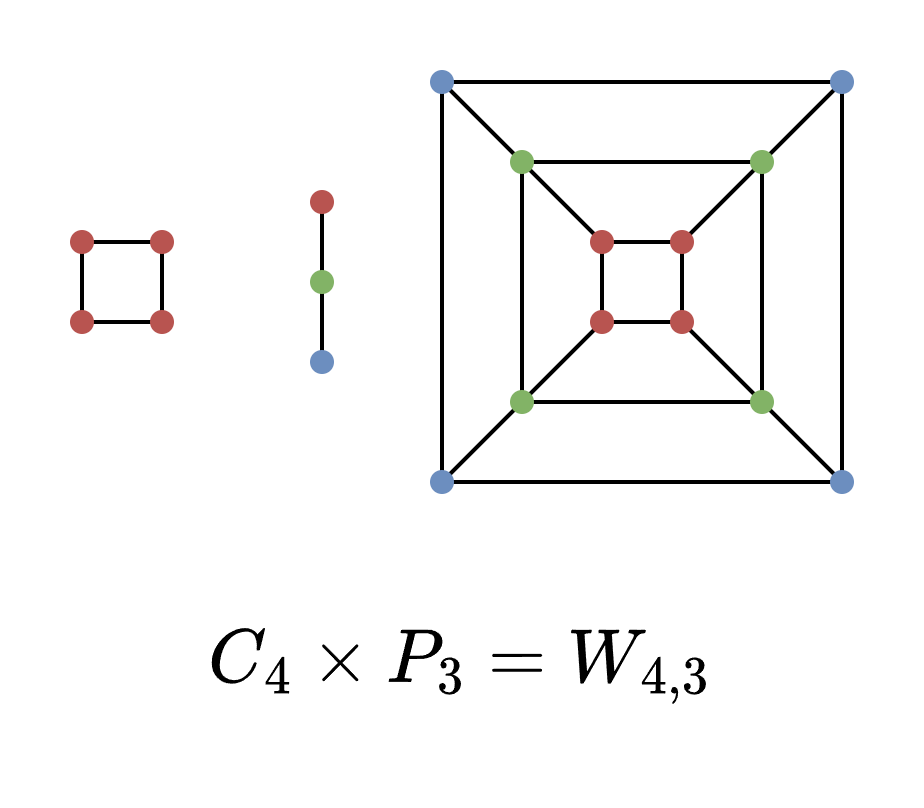
Eliminación de Vértice/Arista

Definimos la operación de vértices o aristas, como $G-e_i$, o $G-v_i$. Si es indiferente que vértice se elimina, dando grafos isomorfos, se omite la identificación del vértice, en tal caso podemos anotar la igualdad con $=$ en lugar de $\cong$.

$$K_4-v=K_3$$

Dado un grafo $G$, su deck es un multiconjunto de subgrafos (posiblemente repetidos), obtenidos de la eliminación de exactamente un vértice. El edge-deck de un grafo es el conjunto de clases isomórficas de su deck. Más generalmente, se puede tener un deck de vértices y un deck de aristas.

Si un grafo puede ser reconstruido a partir de su deck, se dice que es reconstruible. Esto es, si un grafo es inequívocamente determinado por sus deck*.*

Grafo Dual

Dada una inmersión de un grafo $G$, se define su dual $G^{\ast }$ al grafo que tiene tantos vértices como caras del original, existiendo una arista entre dos vértices del dual por cada arista de frontera entre las correspondientes caras del original. El dual del dual se llama bidual, y se denota $G^{\ast \ast }$.

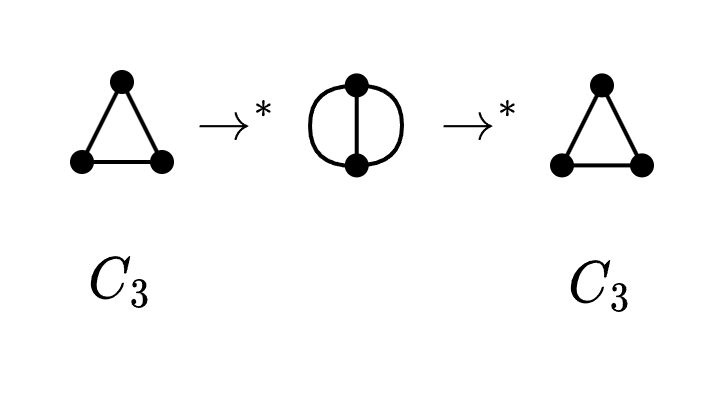
Se observa que C_3^{**} \cong C_3$$C_3^{**} = C_3, pero en general no se puede decir que $G^{\ast \ast }\cong G$. Esto ocurre si el original es conexo $(2P_2^{\ast \ast }≆2P_2)$

Sean $G,H$ dos inmersiones isomorfas, entonces no necesariamente se cumple que $G^{\ast }\cong H^{\ast }$.

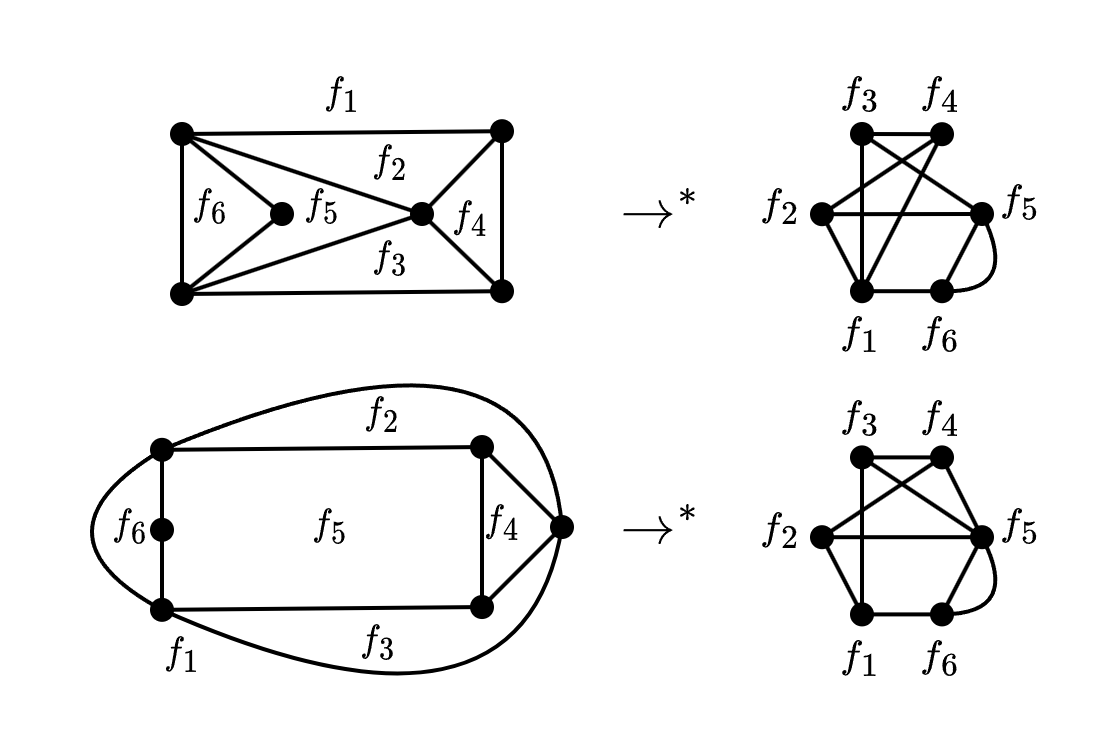
Podemos observar en este ejemplo que los grafos iniciales son isomorfos, pero los grafos duales no lo son (tienen distinto grado máximo).

Curiosamente, observamos que los grafos resultantes son planares.

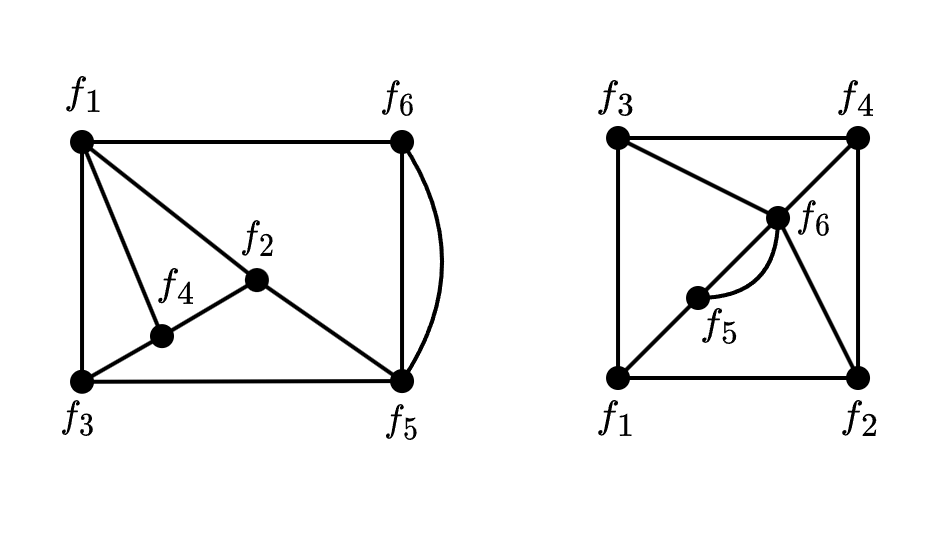
Observación

El dual siempre es conexo, por la definición de cara.

Grafo Arista

Dado el grafo sin lazos $G$, se define su grafo arista $L$ como el grafo tal que sus vértices sean las aristas de $G$, y dos vértices son adyacentes si y solo si sus aristas asociadas al grafo original incidían sobre el mismo vértice.

Sea $u$ el vértice de $L(G)$ asociada a las aristas $xy$ de $G$, siendo $x$ e $y$ dos vértices, entonces el grado de $u$, $d(u)$ estará dado por el grado de ambos vértices $x,y$. Sin embargo, debemos descontar dos vecinos, ya que estos estarán contados en la propia arista.

$$d(u)=d(x)+d(y)-2$$

Si $G$ es isomorfo a $L(G)$, entonces (y la recíproca es verdadera) $G$ es $2$-regular. Esto implica que es un ciclo, o una suma disjunta de ciclos.

Si $G$ un grafo de orden $n$ y tamaño $m$, con sucesión de grados $d(G)=(d_1,d_2,\cdots ,d_n)$, entonces se cumplirá que, por definición

$$n(L(G))=m(G)$$

Cada arista estará asociada a todos el resto de aristas incidentes en un vértice, esto implicará que para cada vértice $u$, se obtendrá un sub-grafo completo de orden $d(u)$ en el grafo arista

$$m(L(G))=\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{d_k}{2}\right)=\frac{1}{2}\sum _{k=1}^n{d}_k^2-m$$

Si un grafo $G$ es euleriano, entonces por la propia definición, su grafo arista $L(G)$ es hamiltoniano. Además, será euleriano, ya que todos los vértices tendrán un grado par (debido a que los vértices asociados al grafo original también tendrán un grado par).

Si un grafo $G$ es hamiltoniano, entonces su grafo arista $L(G)$ también lo será. Sea $H$ el ciclo hamiltoniano al grafo original, entonces podremos partir de ese ciclo y, para cada vértice, agregar al recorrido las aristas que no pertenezcan al ciclo. Debido a que todas las aristas incidentes en un mismo vértice son adyacentes, podremos agregar las aristas al recorrido y continuar el recorrido actual. Luego, obtendremos un camino que recorre todos los vértices del grafo arista.