Iteración en un Punto Fijo

$$P\text{ es punto fijo si }f(P)=P\text{ siendo }f\in \mathcal{C}[a,b]\text{ y }P\in [a,b]$$

Geométricamente, el punto fijo se encuentra cuando la función corta la recta $y=x$

Teoremas del Punto Fijo

Teorema 1.1: Si $f\in \mathcal{C}[a,b]$ y $f(x)\in [a,b]\forall x\in [a,b]$ entonces existe punto fijo

Teorema 1.2: Si $\exists 0<k<1/\Vert f’(x)\Vert \le k\forall x\in [a,b]$, entonces el punto fijo es único.

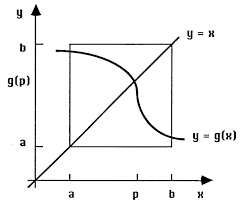
Si la función es siempre creciente o decreciente a razón menor a uno, entonces cortara con la recta $y=x$ únicamente una vez.

Teorema 2: A partir del teorema 1.2, para cualquier $p_0\in [a,b]$, la sucesión $p_n=g(p_{n-1})$ converge al punto fijo.

La convergencia es monótona si la derivada es positiva, la convergencia es oscilatoria si la derivada es negativa. Si las derivadas no cumplen las condiciones del teorema, entonces divergen de forma monótona u oscilatoria, dependiendo de su signo.

Cota de Error

Puedo demostrar con el teorema del punto fijo, que el número de iteraciones del algoritmo cumple la siguiente inecuación. Siendo $k$ la derivada máxima de la función en el intervalo.

$$\Vert p_n-p\Vert \le \frac{k^n}{1-k}\Vert p_1-p_0\Vert <\epsilon$$

Puedo despejar $n$ para obtener cuantas veces debo iterar la sucesión para obtener una tolerancia deseada.

Búsqueda de Raíz

Si buscamos $p$ tal que $f(p)=0$, podemos definir $g(x)=x-f(x)$. Por lo que buscar las raíces de $f$ equivale a buscar los puntos fijos de $g$.

Análogamente, si $g(p)=p$, entonces $p$ es raíz de $f(x)=g(x)-x$

Sin embargo, la función $g$ debe ser admisible. Debe cumplir las condiciones del Teorema del punto fijo.