Algoritmos

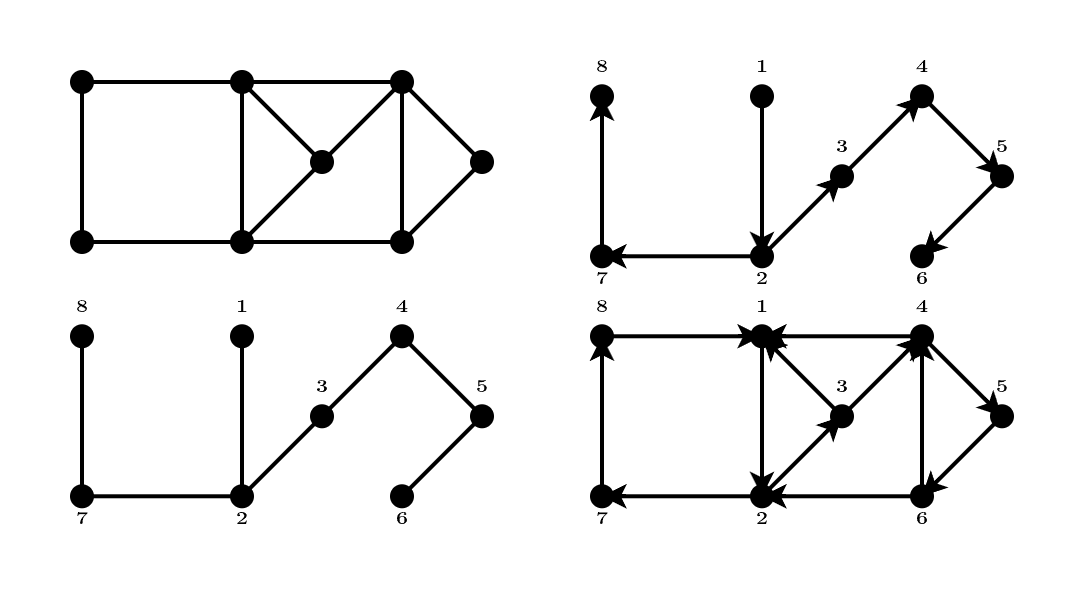
DFS

El algoritmo Depth First Search (DFS) es un algoritmo que busca encontrar una orientación fuertemente conexa para un grafo:

1. Se elige un vértice $v$ cualquiera, y se lo etiqueta como el primero
2. Se toma un vértice cualquiera, adyacente al anterior.
3. Se avanza en profundidad, cuidando de no crear ciclos, formando un árbol generador. Cada vértice se etiqueta en orden que se recorre.
4. Se orienta cada arista que es parte del árbol generador, de menor a mayor. Las agregan las aristas que no son parte de árbol generador, orientándolas del vértice mayor al vértice menor, a partir de la secuencia definida previamente.

Prim

El algoritmo de Prim es un algoritmo que busca generar un árbol generador mínimo; esto es, a partir de un grafo pesado, genera un árbol generador que minimice la suma del peso de sus aristas.

1. Parto de un vértice cualquiera del grafo.
2. Mientras queden vértices sin conectar, agrego la arista mínima, conectada con el grafo actual, que incida sobre un vértice aún no seleccionado.
3. Una vez conecte todos los vértices, tendré un árbol generador mínimo.

El árbol generado no es único, pero su peso será el mínimo posible.

Kruskal

El algoritmo de Kruskal es un algoritmo que, al igual que el algoritmo de Prim, busca generar un árbol generador mínimo.

1. Parto de una arista de peso mínimo
2. Mientras pueda, agrego la arista mínima que no genere ciclos.
3. Una vez no tengo más aristas para agregar, tendré un árbol generador mínimo.

Dijkstra

El algoritmo de Dijkstra busca, para un vértice $v$, el camino de longitud mínima hacia el resto de vértices del grafo. Para hacerlo, requiere los siguientes elementos:

• Un vector de vértices visitados del grafo: $V$.
• Un vector de vértices no visitados del grafo: $NV$.
• Una tabla de distancias en la que, para cada nodo, se guarda su distancia al origen y el vértice por el cual se llega a él. Inicialmente, la distancia a cada nodo será infinito, excepto el vértice del origen. La columna de vértice anterior estará inicialmente vacía.

El algoritmo es el siguiente:

1. Elijo el vértice no visitado con menor distancia conocida en la tabla, inicialmente este será el vértice elegido como inicial. Marco el vértice actual como visitado
2. Para cada vértice adyacente, calculo su nuevo distancia como la distancia al nodo actual, más la distancia del nodo actual al vértice adyacente. Si esta distancia es menor a la indicada, entonces actualizo la distancia del vértice adyacente, denotando el vértice actual como el anterior.
3. Repito hasta haber visitado todos los vértices
4. Puedo calcular la distancia del nodo inicial a todos los nodos a partir de reconstruir los caminos de forma inversa. Tomo un nodo, voy a su nodo marcado como anterior, repito hasta alcanzar el nodo inicial. Luego, puedo reconstruir el camino del nodo inicial al nodo deseado.

Ford-Fulkerson

Una red de transporte es un dígrafo $G$ conexo y sin lazos, donde se verifica que:

• Existe un vértice $O$ fuente tal que solo tiene aristas salientes
• Existe un vértice $T$ sumidero tal que solo tiene aristas entrantes
• Existe una función $C:E(G)\to N_0$ que indica para cada arista, su capacidad de transmisión de flujo.

Se le llama flujo de $G$ a una función $F:E(G)\to N_0$ tal que su valor siempre sea menor a la capacidad de dicha arista, y el flujo entrante y saliente a cada vértice debe ser el mismo (exceptuando la fuente y el sumidero)

Buscaremos la cantidad de flujo máximo que podremos transportar desde la fuente al sumidero, y el camino óptimo para realizarlo.

1. Establecemos como condición inicial, $\Phi =0$
2. Mientras haya un camino de aumento desde $O$ hacia $T$. Estos los podemos encontrar colocándonos en el sumidero y analizar un camino posible de llegada. No debemos considerar aquellos caminos que ya estén saturados (se esté utilizando su capacidad total)
   1. Calcular el cuello de botella del camino. Esto es la máxima cantidad de flujo que puedo enviar por allí, es decir, el mínimo de los pesos de las aristas que lo conforman, o en el caso de ser aristas ya utilizadas, el mínimo de la capacidad libre restante de cada una.
   2. Actualizar el flujo a través de cada arista, denotando la capacidad en uso actual, y la capacidad libre restante.
   3. Actualizar el flujo total $\Phi$, sumándole el valor de cuello de botella calculado anteriormente.