Redes de Petri

Una red ordinaria de Petri es un grafo dirigido bipartito, que cumple con:

PN = (T, P, A)

Donde tenemos:

Un conjunto de nodos $T = t_{1}, t_{2}, ..., t_{n}$ llamados transiciones
Un conjunto de nodos $P = p_{1}, p_{2}, ..., p_{n}$ llamados lugares
Un conjunto de arcos $A \subseteq (T \times P) \cup (P \times T)$

Mostramos un ejemplo sencillo:

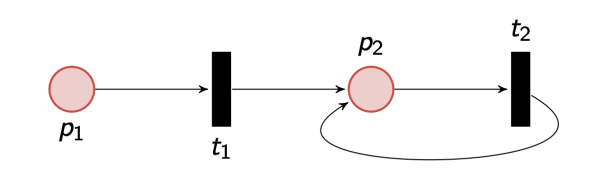
Donde $p_{i}$ son los estados de un sistema, y $t_{i}$ son los eventos que ocasionan los cambios de estado.

Función de Marca

Se define la función de marca $M$ como la cantidad de tokens que hay en cada uno de los lugares de la red de Petri.

M : P \to N_{0}

Cuando hay un único token que está en el lugar $p_{1}$ , entonces $M (p_{1}) = 1$ , y $M (p_{2}) = 0$ , por lo tanto, $M_{0} = (1, 0)$ (para el caso del ejemplo anterior)

Funciones de Entrada y Salida

Sea $t$ una transición perteneciente a la red de Petri.

Se define la función $I (t) = {p \in P ∣ (p, t) \in A}$ como la entrada de la transición $t$ . El conjunto de lugares que pueden derivar en esa transición. Es necesario que haya un token en todas las entradas de una transición para poder activarla.
Se define la función $O (t) = {p \in P ∣ (p, t) \in A}$ como la salida de la transición $t$ . El conjunto de lugares al que se deriva un token a través de la transición $t$ . Se genera un token para cada salida de una transición.

Grafo de Alcance

Un grafo de alcance determina la función de marca para cada estado de la ejecución.

A partir de una red de Petri cualquiera:

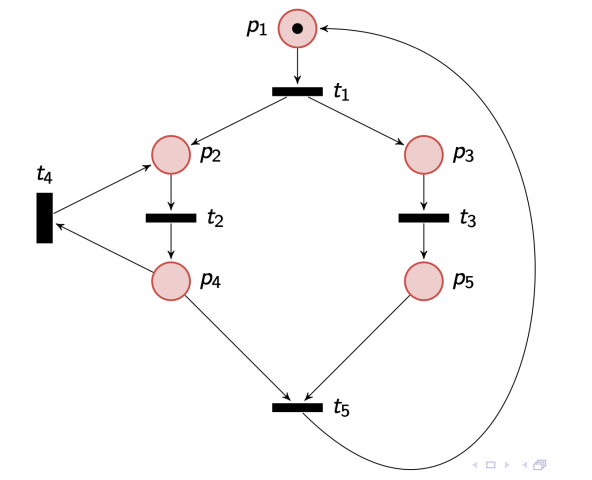
Podemos diagramar su grafo de alcance:

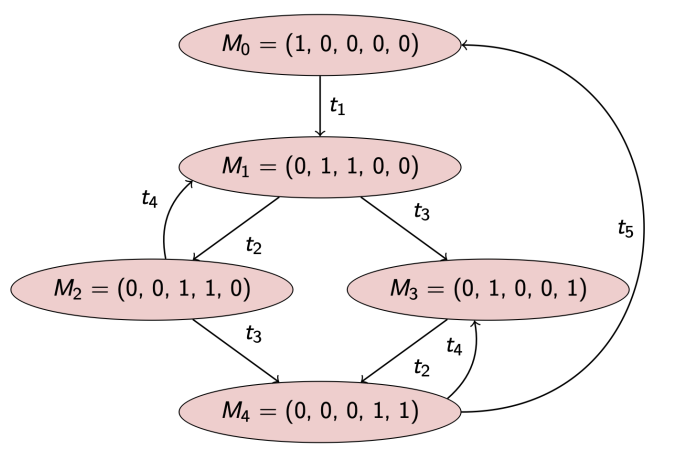
Si encontramos que un estado del grafo de alcance no tiene ninguna arista saliente, diremos que estamos en un deadlock.

Utilidades

Las redes de Petri nos permiten realizar un análisis estático del sistema, para detectar la existencia de deadlocks.

Redes Generales de Petri

Una red general de Petri es un grafo dirigido bipartito, que cumple con:

PN = (T, P, A, W, M_{0})

Donde tenemos:

Un conjunto de nodos $T = t_{1}, t_{2}, ..., t_{n}$ llamados transiciones
Un conjunto de nodos $P = p_{1}, p_{2}, ..., p_{n}$ llamados lugares
Un conjunto de arcos $A \subseteq (T \times P) \cup (P \times T)$
Una función de peso $W : A \to N$
Una función de mara inicial $M_{0} : P \to N_{0}$

Transiciones

El peso de un arco nos indica la cantidad de tokens que consume (entrada) o produce (salida) la utilización del arco (y de su transición).

La transición $t$ está habilitada si y solo si $M (p) \geq W (p, t) \forall p \in I (t)$ . Cuando $t$ se dispara:

$\forall p \in I (t) : M (p) \leftarrow M (p) - W (p, t)$
$\forall p \in O (t) : M (p) \leftarrow M (p) + W (p, t)$

Arco Inhibidor

Un arco inhibidor es aquel que solo permite una transición cuando el lugar no tiene ningún token.

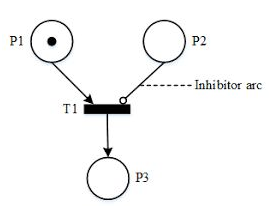
Esto permite modelar problemas más complejos como el Problema del Lector-Escritor.

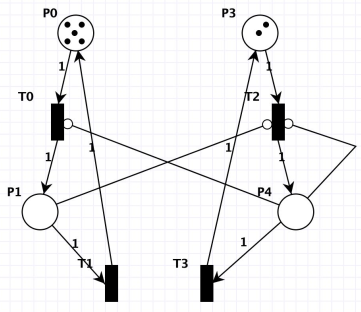
Donde los lugares representan:

En $P 0$ están los lectores a la espera de acceder a la sección crítica.
La transición $T 0$ representa la entrada a la sección crítica de los lectores.
En $P 1$ están los lectores en la sección crítica. Si hay lectores, se inhibe la transición $T 2$ de los escritores.
La transición $T 1$ representa la salida de la sección crítica de los lectores.
En $P 3$ están los escritores a la espera de acceder a la sección crítica.
La transición $T 2$ representa la entrada a la sección crítica de los escritores.
En $P 4$ están los escritores en la sección crítica. Si hay escritores, se inhibe la transición $T 2$ de los escritores, y la entrada $T 0$ de los lectores.
La transición $T 3$ representa la salida de la sección crítica de los escritores.

Apuntes

Explorador