Dieléctricos

Los aislantes o dieléctricos no poseen electrones libres, por lo que no será posible el desplazamiento de carga a través de ellos.

Modelo Elemental de Dieléctricos

• Cada molécula del material adquiere un momento dipolar eléctrico inducido proporcional al campo externo $\vec{E}$
• Las moléculas poseen una distribución de carga positiva y negativa, por lo que son reorientadas por el campo externo $\vec{E}$. En lugar de estar orientadas al azar.

Dipolo Puntual

Está formado por dos cargas $q$, del mismo módulo y signo opuesto, separadas una distancia $\delta$. Nos interesa el campo del dipolo para valores mucho mayores que $\delta$.

Momento Dipolar $p$: Vector cuyo módulo es el producto $(q\cdot \delta )$ y tiene la dirección de la recta que une ambas cargas, apuntando hacia la carga positiva.

Si el dipolo se encuentra en un campo eléctrico, se produce un torque $\tau$ sobre el mismo. Este torque tiende a alinear el dipolo $(p)$ en la dirección del campo externo.

Experimentos de Faraday

Experimento 1

1. Se carga un capacitor en el vacío
2. Se desconecta la pila (carga neta permanece constante)
3. Se introduce un aislante entre los conductores del capacitador

Resultado: La diferencia de potencial entre las placas es menor al de la pila, es decir, aumenta la capacidad del capacitador. (carga constante)

Experimento 2

1. Se carga un capacitor en el vacío
2. Se deja conectada la pila (carga neta puede variar)
3. Se introduce un aislante entre los conductores del capacitador

Resultado: La carga de las placas aumenta, es decir, aumenta la capacidad del capacitador. (diferencia de potencial constante)

¿Por qué ocurre esto?

El dieléctrico se polariza por acción del campo eléctrico del capacitador.

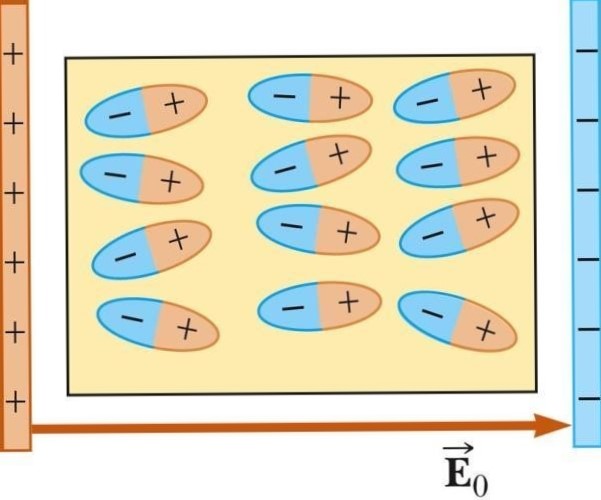
Entonces podemos diferenciar dos tipos de cargas

• $Q_{\text{libres}}\to \text{Vacio, Conductores, Dielectricos (exceso)}$
• $Q_{\text{polarizacion}}\to \text{Dielectricos }:{\delta }_p,{\sigma }_p$

Ahora queremos calcular el campo eléctrico, a partir de la ley de Gauss.

{\subset\!\supset} \llap{\iint}_{S} \vec E \cdot d \vec s = \frac{Q_{enc}}{\epsilon_0}

Como a priori no sabemos las cargas de polarización, entonces vamos a asignar a cada tipo de carga, un campo eléctrico.

$$\begin{array}{rl}& Q_{\text{enc}}^{\text{libres}}⟹\vec{D}:\text{Campo Desplazamiento}\\ & Q_{\text{enc}}^{\text{pol}}⟹\vec{P}:\text{Campo Polarizacioˊn}\end{array}$$ \begin{align*} &\overbrace {\Phi_D = {\subset\!\supset} \llap{\iint}_{S} \vec D \cdot d \vec s = Q_{\text{enc}}^{\text{libres}} }^{\text{Ley de Gauss Generalizada}} \implies \vec \nabla \vec D = \delta^{\text{libres}} \\ &\Phi_P = {\subset\!\supset} \llap{\iint}_{S} \vec P \cdot d \vec s = -Q_{\text{enc}}^{\text{pol}} \implies \vec\nabla \vec P = -\delta^{\text{pol}} \end{align*}

Si combinamos estas definiciones, llegamos a la relación constitutiva:

$$\vec{E}=\frac{\vec{D}-\vec{P}}{{\epsilon }_0}⟺\vec{D}={\epsilon }_0\vec{E}+\vec{P}$$

Note

Podemos ver que el campo eléctrico se reduce debido al campo de polarización, por lo que la diferencia de potencial entre las placas será menor.

Permitividad Dieléctrica Relativa

Es un factor que representa la relación entre la densidad de cargas antes y después de introducir un dieléctrico.

$$\delta ={\delta }_0+{\delta }_{\text{pol}}$$ $$\frac{\delta }{{\delta }_0}={\epsilon }_r$$ $$E={\epsilon }_r{E}_{0}C={\epsilon }_r{C}_0$$

La permitividad indica el cambio en el campo eléctrico dentro del dieléctrico, lo que a su vez modifica la capacidad del capacitor.

¿Hay alguna relación entre los campos eléctricos?

Ya que los medios materiales con los que trabajamos en Física II son LIH Podemos obtener la siguiente relación.

$$\vec{D}=\epsilon \cdot \vec{E}\epsilon ={\epsilon }_0\cdot {\epsilon }_r$$

Siendo $\epsilon$ la permitividad eléctrica del material, y ${\epsilon }_r$ la permitividad dieléctrica relativa. $({\epsilon }_r\ge 1)$.

A partir de la relación constitutiva, podemos llegar a la siguiente fórmula.

$$P={\epsilon }_0\cdot ({\epsilon }_r-1)\cdot \vec{E}{\epsilon }_r-1=X_E$$

Siendo $X_e$ La susceptibilidad dieléctrica. $(X_E\ge 0)$.

Campo Desplazamiento a $Q$ constante

El campo desplazamiento está generado solo por las cargas libres, por lo que el campo desplazamiento con o sin dieléctrico es el mismo.

Siendo $E_0$ el campo eléctrico sin dieléctrico y $E$ el campo eléctrico con dieléctrico, entonces:

$$\vec{E}=\frac{{\vec{E}}_0}{{\epsilon }_r}$$

Vemos entonces como afecta a la capacidad y al potencial de un capacitor:

$$\Delta V=\frac{\Delta V_0}{{\epsilon }_r}⟺C={\epsilon }_r\cdot C_0$$

Campo Desplazamiento a $\Delta V$ constante

Si la diferencia de potencial es constante, entonces el campo eléctrico con y sin dieléctrico es el mismo, por lo que podemos llegar a la siguiente definición, a partir de la relación entre los campos.

$$\vec{D}={\epsilon }_r{\vec{D}}_0$$

Como la diferencia de potencial es constante, entonces ahora lo que cambia son las cargas:

$$Q={\epsilon }_r\cdot Q_0⟺C={\epsilon }_r\cdot C_0$$

Cargas de Polarización

Las cargas del dieléctrico se dividen en dos. Las cargas en la superficie, y las cargas en el volumen

Por lo tanto, tenemos:

• ${\rho }_p:\text{Densidad Volumetrica}$
• ${\sigma }_p:\text{Densidad Superficial}$

Cargas Volumétricas

A partir de la ley de Gauss en su forma diferencial, y las relaciones anteriormente mencionadas, podemos relación la densidad volumétrica de cargas polarizadas con la densidad volumétrica de cargas libres en el dieléctrico

$${\rho }_p=\frac{-X_e}{{\epsilon }_r}\cdot {\rho }_{libres}$$

Si el dieléctrico está descargado, entonces la densidad volumétrica de cargas polarizadas es nula.

Cargas Superficiales

A partir de la ley de Gauss en su forma integral, podemos calcular el flujo del campo polarización en la superficie (con un largo de altura infinitesimal).

$${\sigma }_p=\vec{P}{|}_S\cdot {\hat{n}}_s$$

Ruptura Dieléctrica

Todos los dieléctricos tienen un punto en el que se rompen, y dejan de tener sus propiedades. Este punto es el campo máximo. También se da como el máximo voltaje operativo, que se refiere al máximo diferencial de potencial que acepta un dieléctrico.