Grafos Particulares

$N_n:$ Grafo nulo de orden $n$

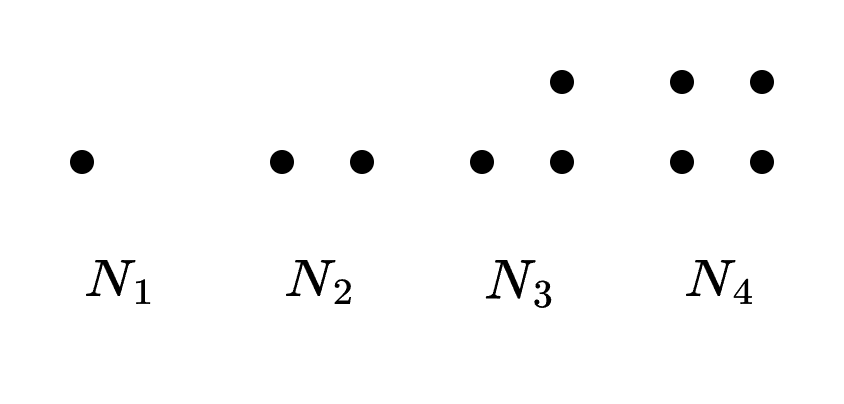
$K_n:$ Grafo simple completo de orden $n$

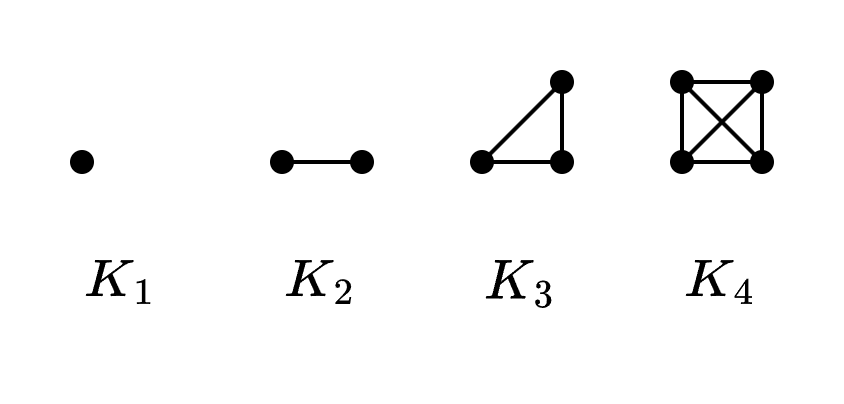
$P_n:$ Camino simple de longitud $n$

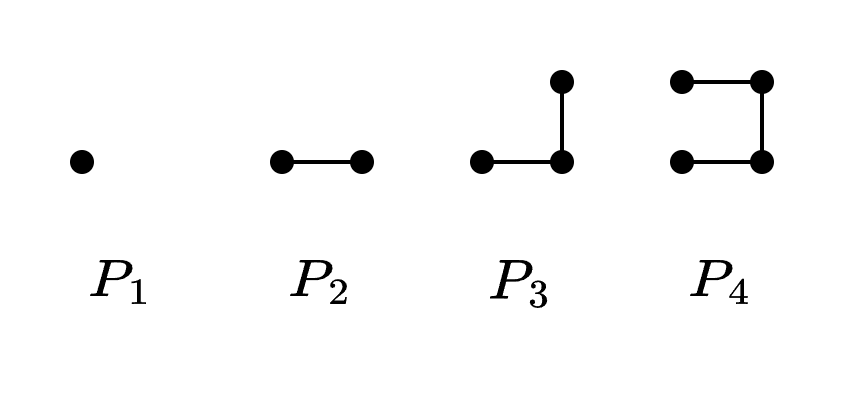
$C_n:$ Ciclo de longitud $n$

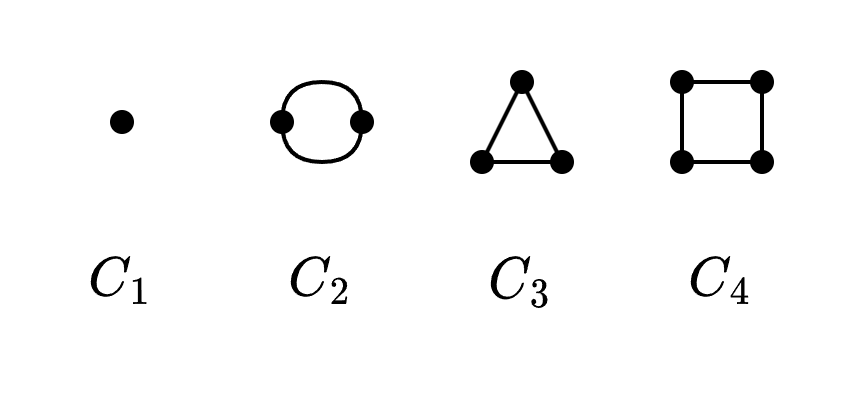
$S_n:$ Estrella

Grafo simple conexo de $n$ vértices con un único vértice de grado $n-1$ que se conecta con los $n-1$ restantes vértices de grado $1$

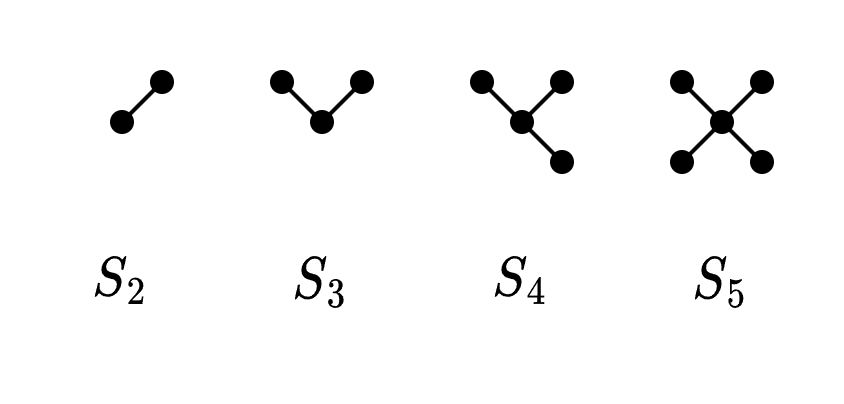
$W_n:$ Rueda

Puede pensarse coloquialmente como una estrella y un ciclo en los satélites.

$\text{Peon}$

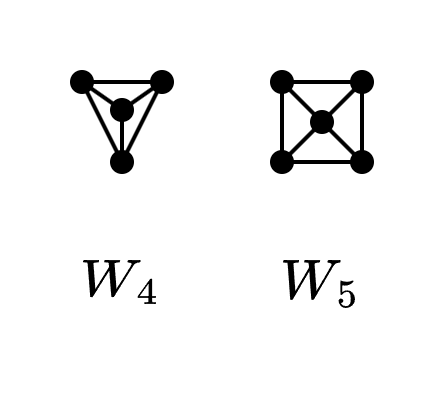
Este es un grafo común, utilizado para demostrar muchas propiedades:

$2p\text{-Corona}$

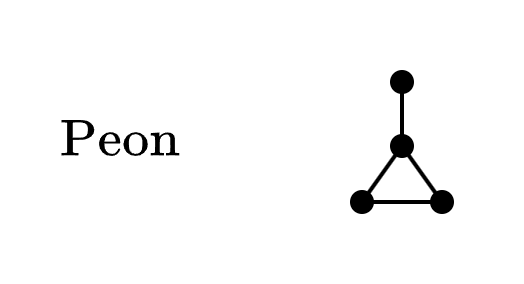
Una $2p$-corona es un bipartito $G(U,V)$ tal que $u_i{v}_j\in E(G)⟺i\ne j$

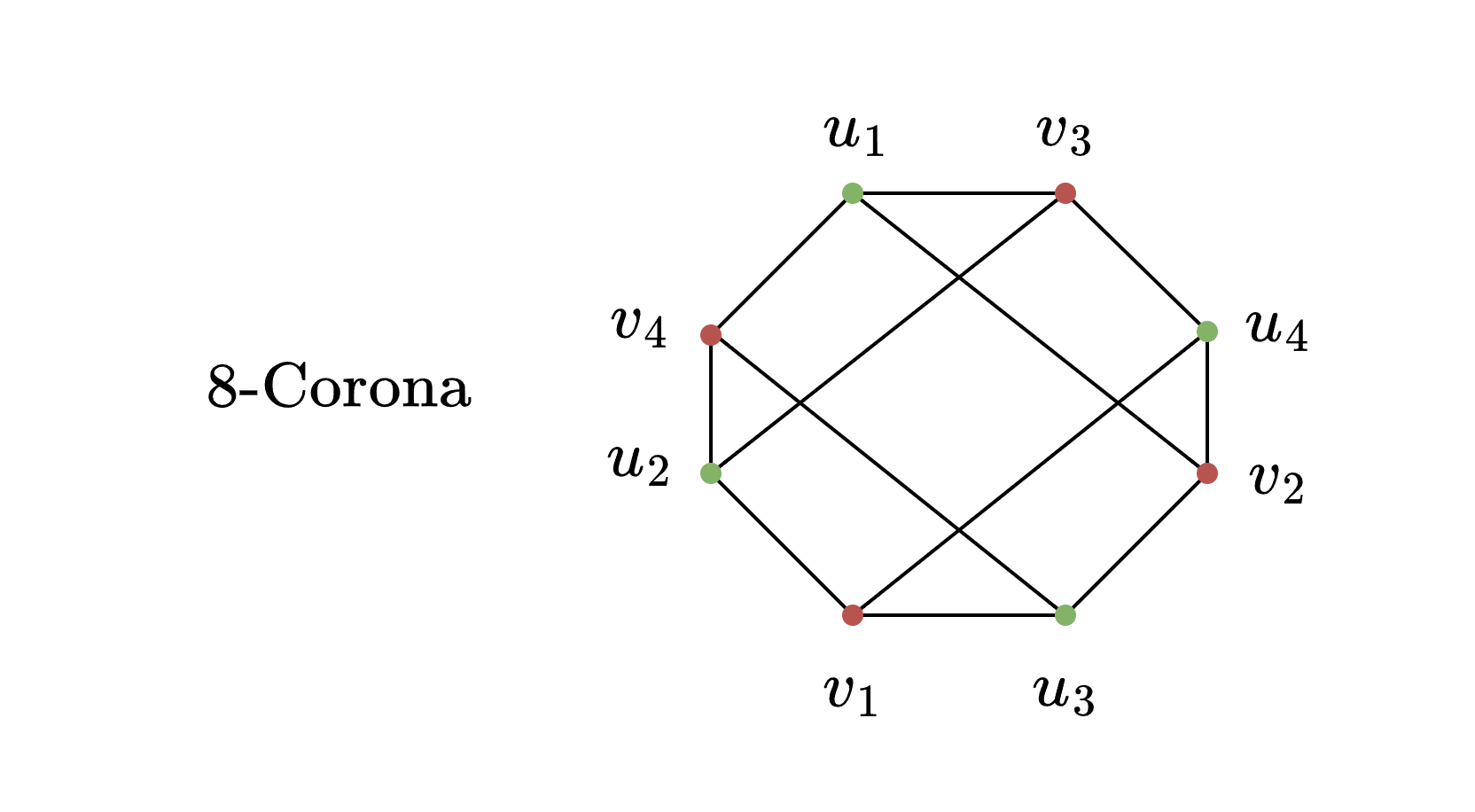
Este grafo será bipartito por su propia definición, pero no será completo (podemos observarlo en la figura

$p\text{-Book}$

Definido como $p$ ciclos $C_4$ todos compartiendo una arista en común. Puede ser definida a partir de operaciones, como $B(p)=S_{p+1}\times P_2$.

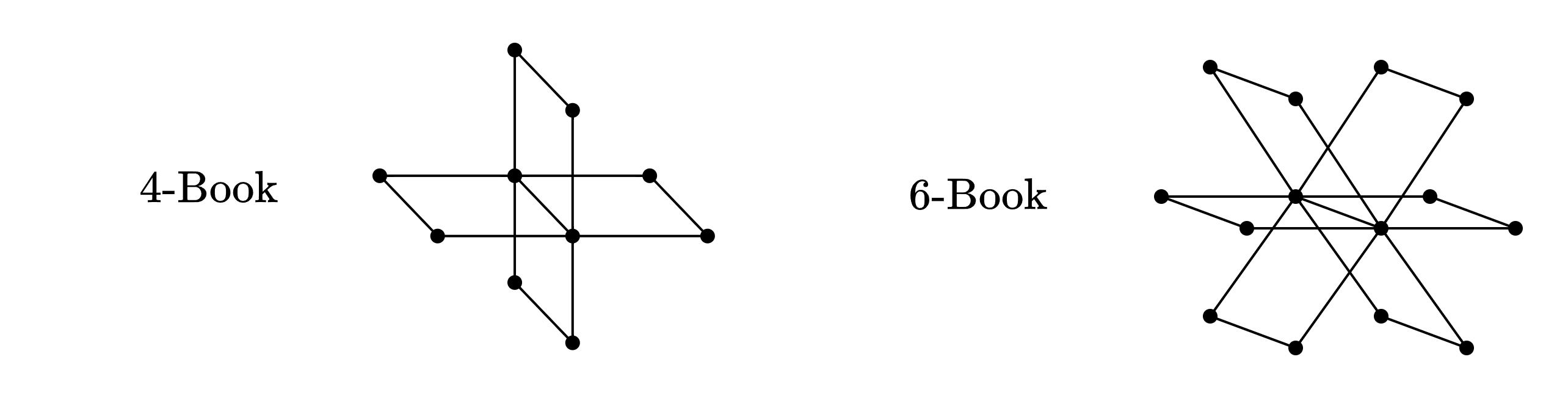
Los libros son bipartitos, ya que las estrellas lo son, y los vértices de cada estrella solo son adyacentes a sus análogos en la segunda estrella. De esta forma, se pueden colorear inversamente las estrellas, formando un grafo bipartito

$p\text{-Cube}$

Grafo con $2^p$ vértices. Los vértices se etiquetan con una cadena binaria de $p$ dígitos, con una arista si la distancia hamming es 1. Alternativamente, puede pensarse con el producto cartesiano de $p$ veces $K_2$

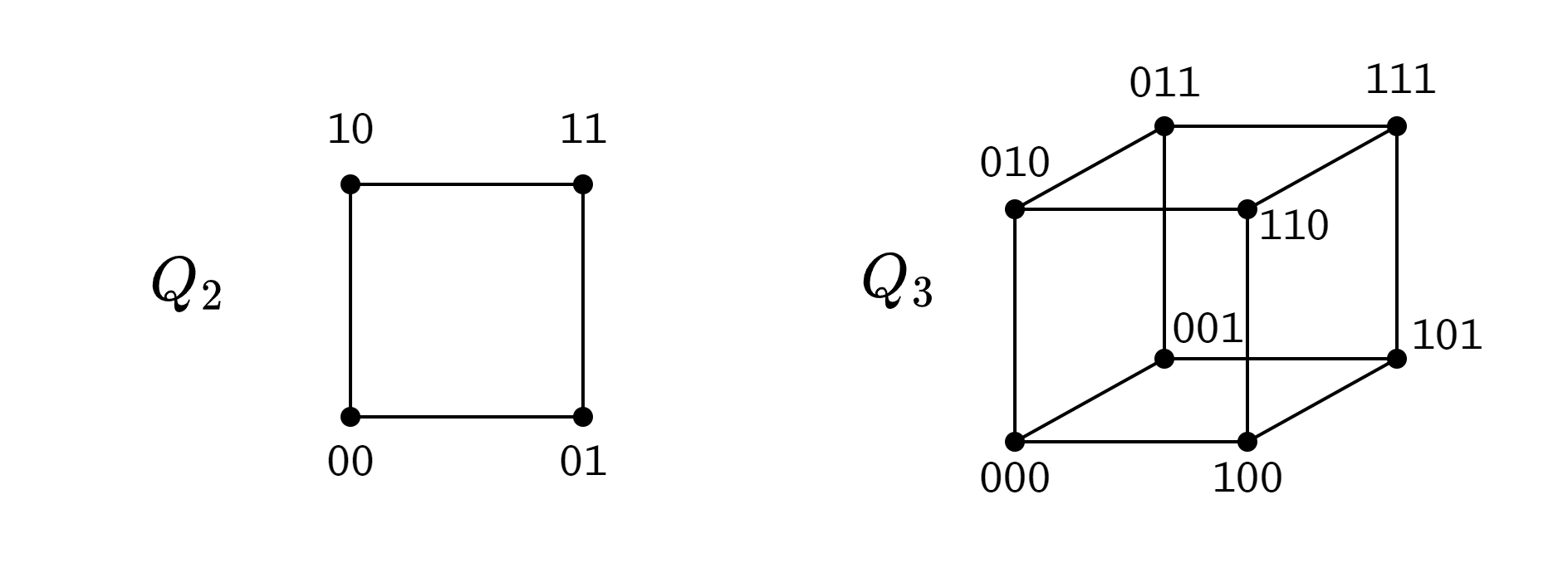
La distancia hamming entre dos cadenas indica la cantidad de bits distintos

$W_d(p,q):$ Molino

Se define como un molino de $q$ aspas de longitud $p-1$, puede formarse con el ensamble $W_d(p,q)=N_{1}q{K}_{p-1}$

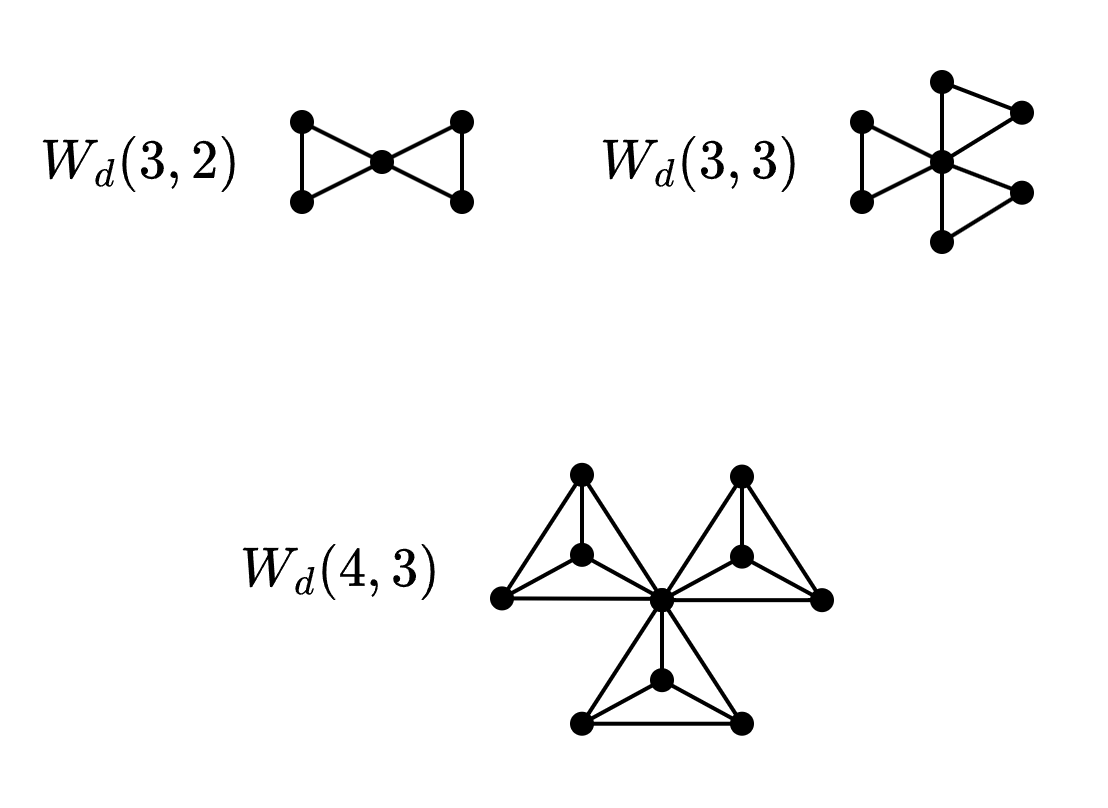
$F(p,q):$ Abanico

El abanico se define por $F(p,q)=N_p{P}_q$

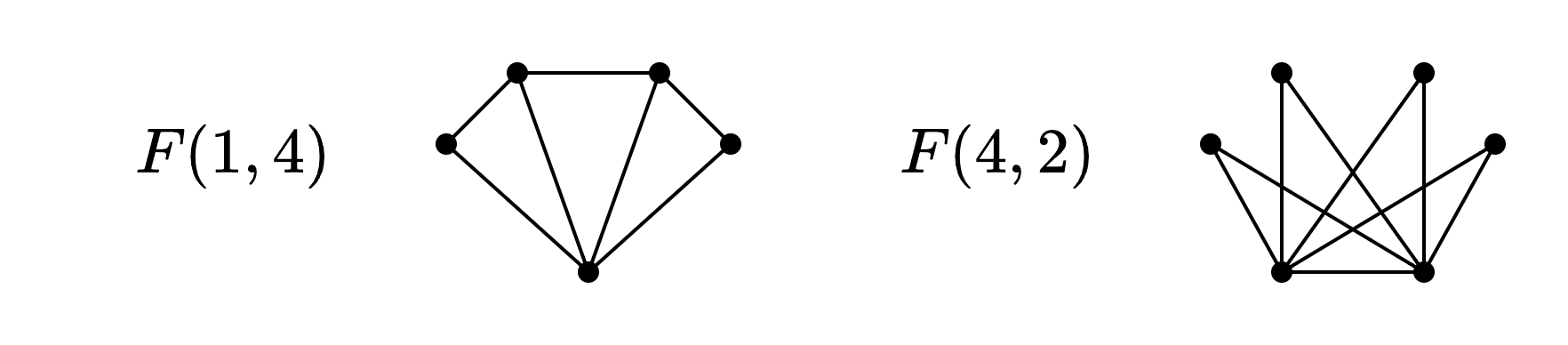
$L_{p,q}:$ Lollipop

Es el grafo simple compuesto por el $K_p$ y el grafo $P_q$ conectados por un puente

$T_{p,q}:$ Renacuajo

Es el grafo simple resultante de conectar $C_p$ con $P_q$ mediante un puente

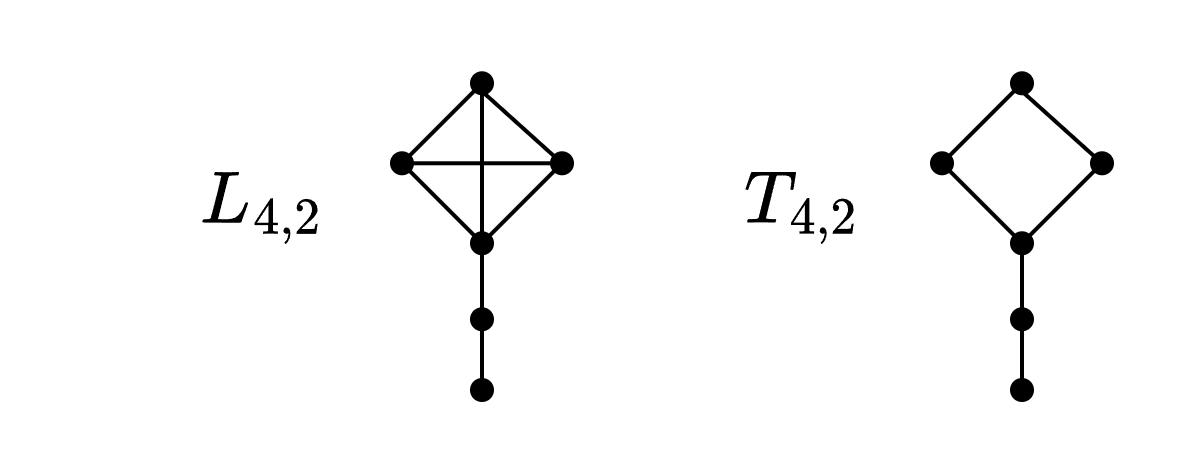
En la imagen, vemos un chupetín a la izquierda, y renacuajo a la derecha

$KP(p,q,l):$ Remo

Es el grafo simple resultante de unir el ciclo $C_p$ con el ciclo $C_q$ mediante un path de longitud $l$.

$B_p:$ Pesa

Es el grafo simple obtenido de conectar dos copias de $k_p$ con un puente

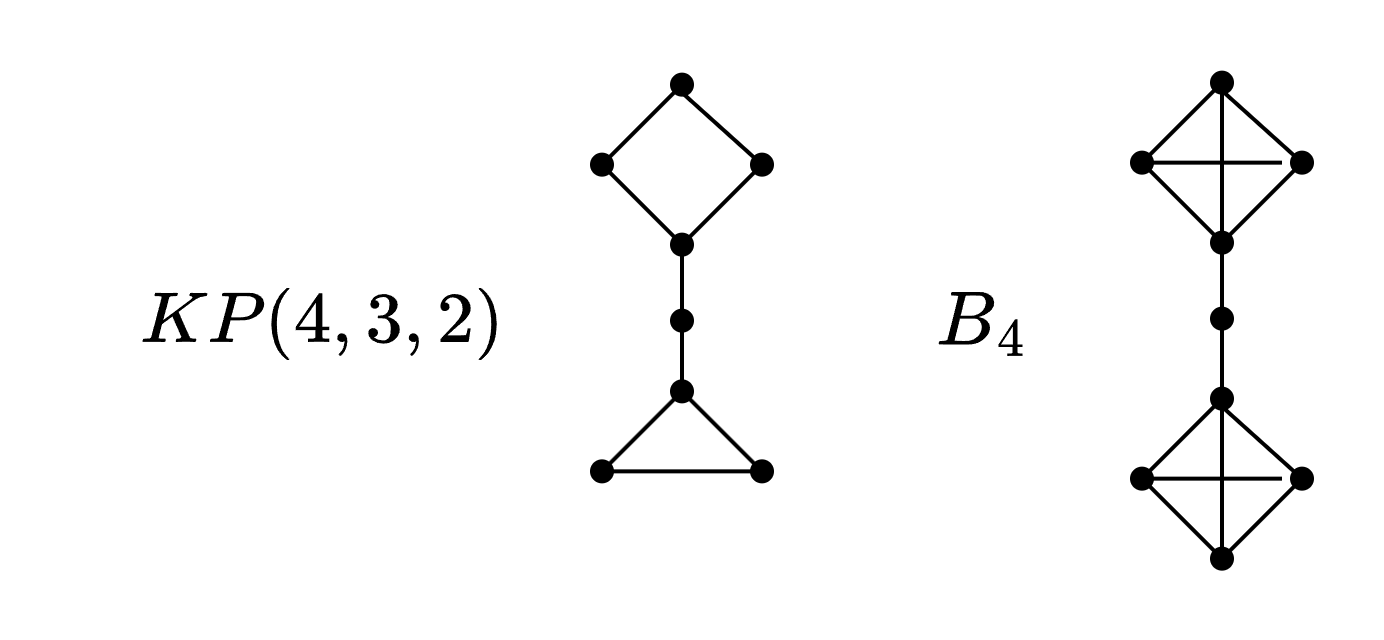
El tamaño del path en los últimos cuatro grafos es referido según su longitud, y no la cantidad de sus nodos

$K(p,q):$ Grafo de Kneser

Dado un $p$-conjunto $H$ fijo, se define el grafo simple $G=K(p,q)$ siendo $V(G)$ = ${\mathcal{P}}_q(H)$ (los $q$-subconjuntos de $H$) con $uv\in E(G)$ si y solo si $uv=\varnothing$. Es decir, dos vértices son adyacentes si y solo si los correspondientes conjuntos son disjuntos. Genéricamente, definimos $K(p,q,s)$ donde $uv\in E(G)$ si y solo si $|uv|\le s$, y entonces particularmente $K(p,q)=K(p,q,0)$.

El miembro ilustre de la familia $K(5,2)$ es isomorfo al grafo de Petersen.

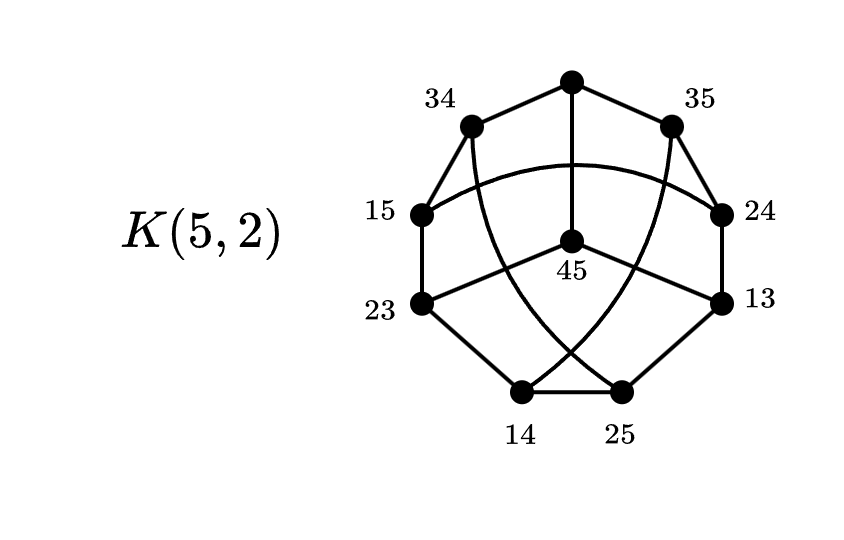
Denotamos $ij$ al vector asociado al conjunto $i,j$

Genéricamente, podemos hallar el tamaño del grafo de Kneser a partir de la cantidad de formas posibles de tomar $q$ elementos de un conjunto de $p$ elementos, es decir,

el número combinatorio

$$n(K(p,q))=\left(\genfrac{}{}{0ex}{}{p}{q}\right)$$

Para las aristas, cada vértice será adyacente a aquellos nodos con los cuales no comparta elementos, luego esto es el número combinatorio $\left(\genfrac{}{}{0ex}{}{p-q}{q}\right)$, Como cada arista se contara dos veces, dividimos el número en dos. Tendremos entonces

$$m(K(p,q))=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{p}{q}\right)\left(\genfrac{}{}{0ex}{}{p-q}{q}\right)$$

Si $q>p$, entonces el grafo será vacío, que es un grafo en sí mismo. La función del grafo vacío se denomina función nula.

Por otro lado, si $p-q<q$, entonces el grafo no tendrá aristas.

$J(p,q):$ Grafo de Johnson

Dado un $p$-conjunto $H$ fijo, se define el grafo simple $G=J(p,q)$ con $q\ge 1$, donde $V(G)={\mathcal{P}}_q(H)$ y $uv\in E(G)$ si y solo si $|uv|=q-1$. Es decir, dos vértices son adyacentes si y solo si la intersección de los conjuntos asociados es de cardinalidad $q-1$. Algunas relaciones particulares son $J(p,1)\cong J(p,p-1)\cong K_p$. El grafo de Johnson generalizo se define como $J(p,q,r)$ donde dos vértices son adyacentes si $|uv|=r$.

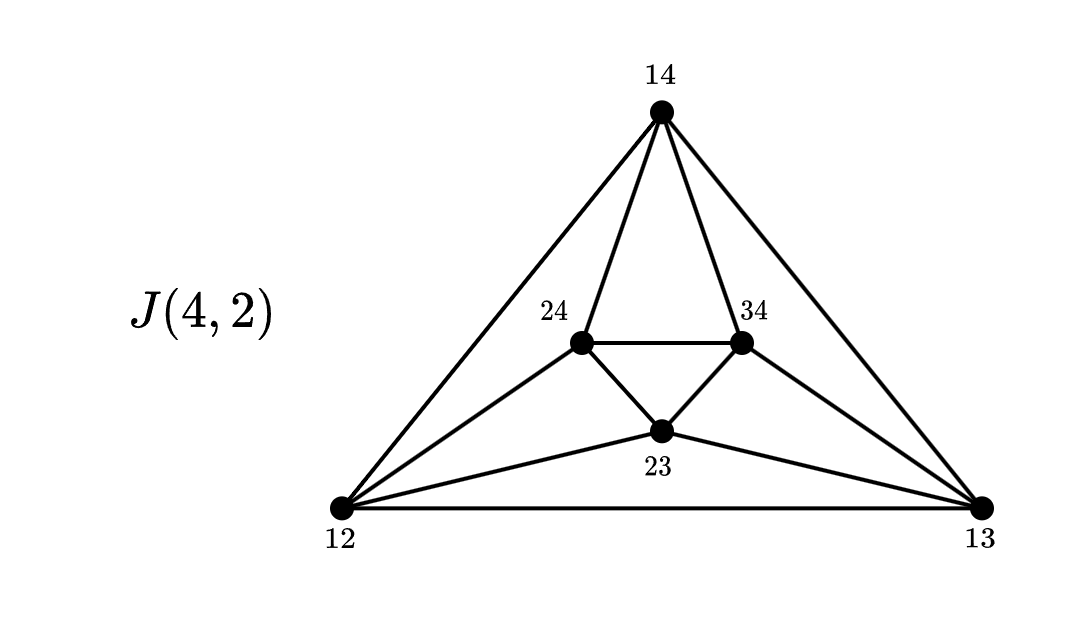
Al igual que con el grafo de Kneser, calcularemos el tamaño del grafo a partir del número combinatorio $\left(\genfrac{}{}{0ex}{}{p}{q}\right)$.

Para calcular el grado de cada nodo, sabemos que por cada elemento del conjunto asociado, podremos conectarnos con los nodos cuyo conjunto asociado difieran en únicamente ese elemento. Como difieren en únicamente ese elemento, este no debe pertenecer al propio nodo, luego $d(v)=q(p-q)$. El cardinal del grafo entonces será:

$$m(J(p,q))=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{p}{q}\right)q(p-q)$$