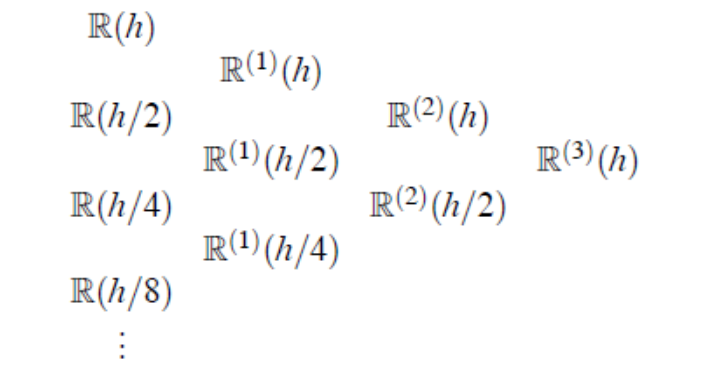Integración Numérica

Newton-Cotes

El método de Newton-Cotes consiste en encontrar el polinomio de Lagrange asociado a los $N+1$ puntos distribuidos en el intervalo $a,b$. Donde $h=x_{k+1}-x_k=\frac{b-a}{N}$

$${\int }_a^{b}f(x)dx\approx {\int }_a^b{P}_L(x)dx=\sum _{k=0}^{N}f(x_k){\int }_a^b{L}_k(x)dx$$

Si llamamos $A_k$ a la integral de $L_k$ sobre el intervalo $a,b$. Entonces

$${\int }_a^{b}f(x)dx\approx \sum _{k=0}^{N}f(x_k)A_k$$

Regla de Los Trapecios

Consiste en aproximar la función a través de $N$ líneas rectas en el intervalo $a,b$, luego calculando el área de todos los trapecios formados. Se utiliza un polinomio de Lagrange lineal para cada intervalo, usando los nodos $x_k,x_{k+1}$

$${\int }_a^{b}f(x)\approx \sum _{k=0}^{N-1}{\int }_{x_k}^{x_{k+1}}{P}_k(x)=\frac{h}{2}[f(a)+f(b)+2\sum _{k=1}^{N-1}f(x_k)]$$

Si $N=1$, se le llama a la regla de los trapecios simple, ya que utiliza un solo trapecio

$${\int }_a^{b}f(x)dx=\frac{b-a}{2}[f(a)+f(b)]$$

Cota de Error

El error se calcula integrando el error de cada uno los polinomios en su intervalo.

$$E_K=\frac{1}{2}{\int }_{x_k}^{x_{k+1}}{f}^{\prime \prime }({\xi }_k(x))(x-x_k)(x-x_{k+1})dx$$ $$E_T=\sum _{k=0}^N{E}_k$$

A partir del teorema del error medio ponderado, encontramos que el error total vale

$$E_T=-\frac{h^3}{12}N{f}^{\prime \prime }(\xi )=-h^2\frac{b-a}{12}{f}^{\prime \prime }(\xi ),\xi \in (a,b)$$

Luego, el orden del error del método de los trapecios es de $O(h^2)$

Regla de Simpson (1/3)

El método es similar, consiste en tomar integrales cada $3$ nodos, usando aproximaciones de Lagrange de grado $2$

$${\int }_a^{b}f(x)\approx \sum _{k=0}^{\frac{N-2}{2}}{\int }_{x_{2k}}^{x_{2k+2}}{P}_k(x)=\frac{h}{3}[f(a)+f(b)+4\sum _{k=0}^{\frac{N-2}{2}}f(x_{2k+1})+2\sum _{k=1}^{\frac{N-2}{2}}f(x_{2k})]$$

Si $N=2$, se conoce como regla de Simpson (1/3) simple, Se reduce a utilizar a integrar un único polinomio de Lagrange con 3 nodos.

El error se calcula integrando el error de cada uno los polinomios en su intervalo.

$$E_K=-\frac{h^5}{90}{f}^{(4)}({\xi }_k)$$ $$E_T=\sum _{k=0}^N{E}_k$$

Luego, el error total del método tiene un orden de $O(h^4)$

$$E_T=-h^5\left(\frac{N}{180}\right)f^{(4)}(\xi )=-h^4\frac{b-a}{180}{f}^{(4)}(\xi ),\xi \in (a,b)$$

Regla de Simpson (3/8)

Para este método, se interpola la función cada intervalos de $4$ nodos. Sin embargo, no hace falta utilizar este método, ya que el orden de su error $O(h^4)$ es igual al de Simpson (1/3).

$${\int }_a^{b}f(x)dx\cong \frac{3h}{8}[f(a)+f(b)+3\sum _{k=0}^{\frac{N-3}{3}}f(x_{3k+1})+3\sum _{k=0}^{\frac{N-3}{3}}f(x_{3k+2})+2\sum _{k=1}^{\frac{N-3}{3}}f(x_{3k})]$$ $$E_T=\frac{b-a}{80}{h}^4{f}^{(4)}(\xi )$$

Método de Romberg

Consiste en usar el método de extrapolación de Richardson para algún método de integración numérica. Resolvemos las integrales con pasos $h,h/2,h/4,\cdots$. Luego utilizamos la extrapolación de Richardson para aproximar la integral.

Tomamos las integrales resueltas como los términos $R^{(0)}(h)$

$$R^{(k)}(h)=\frac{4^k{R}^{(k-1)}(h/2)-R^{(k-1)}(h)}{4^k-1}$$