Aproximación por 2 puntos
Son aproximaciones simples que se realizan a partir de utilizar dos puntos de la función original. Se deducen a partir del teorema de Taylor, despejando la derivada primera e ignorando las derivadas siguientes.
Diferencias Progresivas (adelanto) y Regresivas (atraso)
Se realizan a partir de evaluar en un punto y a una distancia del punto
El error de estos métodos es del orden
Diferencias Centrales
Se realiza a partir de evaluar a una distancia del punto (esta aproximación es igual a la de la derivada centrada en tres puntos, de ahí su orden de error)
El error de este método es del orden .
Aproximación por puntos
A partir de realizar una aproximación por Lagrange, podemos aproximar la derivada usando más puntos.
- Escribo el polinomio de Lagrange con mis puntos. Si tomo los puntos delante del punto será una diferencia progresiva, si tomo puntos detrás del punto será una diferencia regresiva.
- Busco la derivada del polinomio de Lagrange
- Evaluó la derivada en el punto que estoy buscando
El orden del error de este método es de
Cota de Error
La cota de error se encuentra a partir del error de derivar el término del error del polinomio de Lagrange, Si escribimos los puntos en función de , podemos observar el orden del error.
Algunas Derivadas Usadas
Derivada de Órdenes Superiores
A partir de este método, podemos volver a derivar las expresiones para obtener aproximaciones de derivadas de orden superior.
Extrapolación de Richardson
La extrapolación de Richardson consiste en aproximar una derivada a partir de evaluar la función en puntos cada vez más cercanos al punto
-
Planteamos un inicial, evaluamos la función en los puntos de la sucesión
-
Encontramos las aproximaciones para cada uno de puntos
-
A partir de un proceso similar al de las diferencias divididas, encontramos el término a partir de la ecuación
Nuestro árbol de diferencias divididas se verá de la siguiente forma
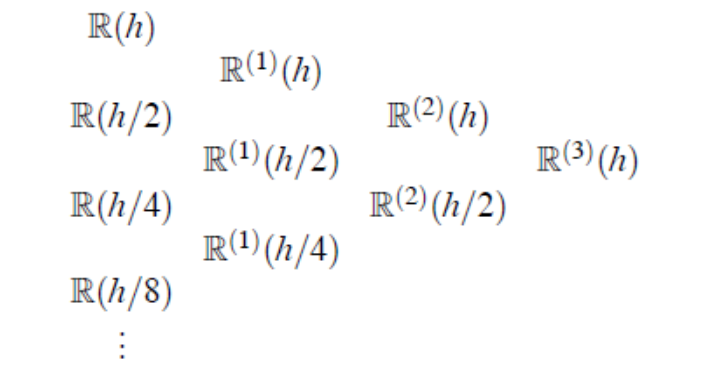
Podemos encontrar que el orden de este método es del orden