Una curva es la imagen de una función vectorial continua en A, donde A es un intervalo de la recta real
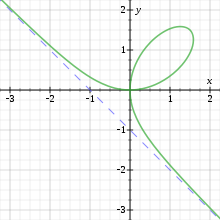
Curva plana
Está totalmente contenida en un plano
Curva cerrada simple
También llamadas curvas de Jordan, solo tienen en común el punto inicial y el final
Tangente a la curva (Regular)
Si existe la derivada en un punto, se puede construir una recta tangente en ese punto. Si se puede derivar en todo el dominio, entonces la curva es regular.
Si se cambia la parametrización de una curva, pueden cambiar las propiedades de su parametrización (tener derivada en un punto que antes no tenía)
Se dice que es regular a trozos si deja de ser regular en un número finito de puntos del intervalo
Plano normal a la curva
El plano perpendicular a la tangente de la curva y que contiene el punto de la misma
Superficies
Una superficie es la imagen de una función vectorial . continúa en
Si dejo constante una de las variables y vario la otra, se genera una curva coordenada
El producto vectorial de los vectores tangentes de 2 curvas coordenadas en un punto en común, te da un vector normal a la superficie
Con el vector normal a la superficie y el punto, puedo encontrar el plano tangente a la superficie
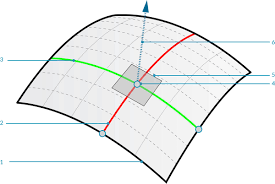
Una superficie es normal si en cada punto de la superficie, se puede encontrar un plano normal a la misma.